いまさら聞けないベイズ推定

ベイズってたまに聞くけど。

ベイズ推定という言葉は聞きなれないかもしれません。その意味では「いまさら聞けない」というタイトルはやや不適切ですが、技術や手法としては機械学習（Machine Learning）¹⁾いまさら聞けない機械学習と同じように広く一般的に使われているものです。もっともベイズ推定は機械学習の手法として利用されるため並列ではありません。

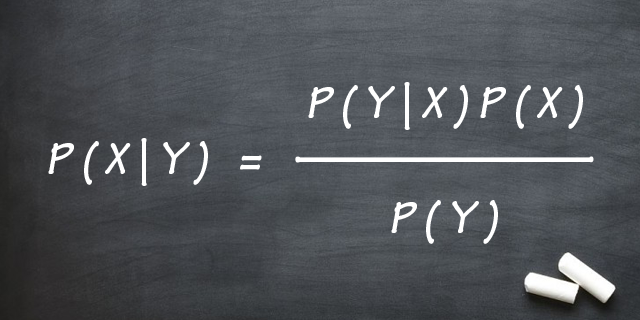
また、ベイズ推定はベイズの定理を基にした推論技術ですが、ベイズ統計、ベイジアンフィルタ、ベイジアンネットワークなど、ベイズの定理を基にした技術や手法はたくさんあるので、なんらか耳にしたことはあるかと思います。これらをひっくるめて簡単に頭の整理をします。

ベイズの定理は、条件付き確率に関して成り立つ定理で、18世紀にイギリスの数学者トーマス・ベイズによって示されたものです。条件付き確率（Conditional Probability）とは、ある事象Xが起こるという条件のもとでの事象Yの確率P(Y|X)のことで、事象Xと事象Yの両方が起こる確率P(X∩Y)と合わせて、事象Xの確率P(X)が正の場合に以下の数式で表現されます。

$$P(Y\mid X) = \frac{P(X\cap Y)}{P(X)}\\$$

ベイズの定理は、ある事象Yが起こった場合の事象Xの確率P(X|Y)を、条件の確率P(X)、結果の確率P(Y)、条件付き確率P(Y|X)から求めることができるというものです。この確率P(X|Y)を逆の条件付き確率といい、確率P(Y)が正の場合に以下の数式で表現できます。なお、条件付き確率の数式を変形したもので、意味はまったく同じです。

$$P(X\mid Y) = \frac{P(Y\mid X)P(X)}{P(Y)}\\$$

つまり、条件の確率P(X)、結果の確率P(Y)、条件付き確率P(Y|X)がわかれば、逆の条件付き確率P(X|Y)を推論できるということです。これで何がうれしいかというと、このような問題を解くことが可能となります。

結果から原因の確率を推論する。

• 今日のゲストが男性か女性かを当てる。
• これまでのデータからゲストが男性である確率は60%である。
• 今日のゲストは身長が165cm以上である。
• 男性が165cm以上である割合は70%、女性が165cm以上である割合は20%である。

身長が165cm以上という情報と、男性のほうが女性よりも165cm以上である割合が高いという情報から、ゲストが男性である確率はこれまでのデータの60%よりも高いと推測されますが、それをベイズの定理で計算してみましょう。

この場合、まず男性に着目すると、条件の確率P(X)は男性である確率の60%、結果の確率P(Y)は身長165cm以上である確率の100%、条件付き確率P(Y|X)は男性の場合に165cm以上である確率の70%となります。すると以下のように、逆の条件付き確率P(X|Y)として男性である確率は42%と計算されます。

$$男性：P(X\mid Y) = \frac{0.7\times 0.6}{1} = 0.42\\女性：P(X\mid Y) = \frac{0.2\times 0.4}{1} = 0.08\\$$

同様に女性に着目すると、女性である確率は8%と計算されるため、男性である確率：女性である確率＝0.42：0.08となり、男性である確率は84%であると推論されます。

このように、ベイズの定理を用いて逆の条件付き確率を求めることで、結果の事象Yが発生した場合に、原因の事象Xが発生している確率を推論する手法をベイズ推定（Bayesian Inference）といいます。

なお、これまでに事象Xが発生した確率P(X)を事前確率、新たに事象Yが発生した場合の事象Xの確率である逆の条件付き確率P(X|Y)を事後確率、条件付き確率P(Y|X)を尤度（ゆうど）ともいいます。また、事後確率を新たな事前確率として扱うことをベイズ更新（Bayesian Updating）といい、繰り返すことで推論精度が上がります。

未知や不確実性に強い。

ちなみに、さきほどから確率（Probability）という言葉を使っていますが、実は二種類の定義があります。頻度確率とベイズ確率です。

頻度確率（Frequency Probability）は、観測された頻度分布あるいは想定された母集団の割合から導かれる確率のことで、客観確率とも言います。また、頻度確率に基づく考え方を頻度主義（Frequentism）、頻度確率に基づく統計を頻度主義統計（Frequentist Statistics）といい、代表的な手法が最尤（さいゆう）推定です。頻度主義統計では母集団を固定するため、母数が定数でデータが変数となります。

ベイズ確率（Bayesian Probability）は、ベイズの定理に基づき、事前確率を事後確率で更新（ベイズ更新）することで得られる確率のことで、事前確率を手元のデータから主観的に決めることから、主観確率とも言います。また、ベイズ確率に基づく考え方をベイズ主義（Bayesianism）、ベイズ確率に基づく統計をベイズ統計（Bayesian Statistics）といい、代表的な手法がベイズ推定です。ベイズ統計では手元のデータを前提とするため、データが定数で母数が変数となります。

頻度主義統計は、充分なデータが得られる場合は客観的な確率を計算できるという特長があるものの、充分なデータが得られない場合には確率を計算できない、母数が更新された場合は最初から計算をしなおす必要があるという欠点があります。一方で、ベイズ統計は、事前確率が手元のデータに依存した主観的な確率であるという欠点があるものの、少ないデータでも確率を推論できる、母数が更新されることが前提かつそれにより推論精度が上がるという特長があるため、未知や不確実性に強く実用的であるといえます。

ベイズ推定の実用例でわかりやすいのはベイジアンフィルタ（Bayesian Filter）です。対象データを分類するフィルタで、学習量が増えるとフィルタの分類精度が上がるという特長があり、スパムメールを判定するフィルタや、検索エンジンのランキングなどで活用されています。また、ベイジアンネットワーク（Bayesian Network）は、複雑な因果関係をグラフ構造で表現し、変数間の関係を条件つき確率で表す確率推論モデルで、これもさまざまな領域で応用されています。

ただ、ベイズ推定がいま最も注目されている領域は機械学習でしょう。「UXモデリングって？」でも触れたように、ビッグデータによる機械学習には、大量の学習データが必要である、導出された予測モデルのメカニズムがブラックボックス化して説明しづらくなるという欠点があります。その克服には正則化が必要ですが、ベイズ推定によるベイズ最適化（Bayesian Optimization）が有効な手法となるため、多層ニューラルネットワークの重みの調整にベイズ最適化を利用する研究がなされています。また、ベイズ最適化と相性のいいカーネル法を活用したサポートベクターマシン（Support Vector Machine：SVM）が見直されています。

またスパースモデリング（Sparse Modeling）²⁾スパースモデリングって？も、スパース条件を事前確率ととらえれば、ベイズ推定の一つであることがわかります。

最後に、ベイス推定を学ぶ参考書として、大関真之氏の著書「ベイズ推定入門 モデル選択からベイズ的最適化まで」をおすすめしておきます。ベイス推定の概念や理論が、数式なしでわかりやすく解説されています。